For this problem, we are told that a certain set of scores is normally distributed with a mean of 71.9 and standard deviation of 10.1 points. We need to determine the score that will determine the boundary for F grades, if they are the lowest 11%.
The first step we need to take is determine the z-score that represent the lowest 11% on the distribuition. We have:
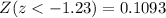
The closest value to 11% on the z-table is a z-score of -1.23, which produces a percentage of 10.93%. With this we can use the expression for the z-score in order to determine the grade that represents this:
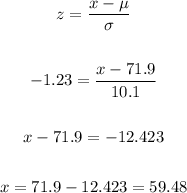
The score that will determine the boundary of the F grade is 59.48.