Question

A 3 cm x 2 cm rectangle sits inside a circle with radius of 4 cm. What is the area of the shaded region? Round your final answer to the nearest hundredth. 3 cm 4 cm 2 cm

Answer 1

The area of the shaded region is equal to the area of the circle minus the area of the rectangle. To determine the said area, you have to calculate the area of the circle and the area of the rectangle first:

Area of the circle

The area of the circle can be determined using the following formula:

`A_O=\pi r^2`

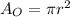
The radius of the circle is r=4cm, then the area can be calculated as follows:

`\begin{gathered} A_O=\pi(4)^2 \\ A_O=16\pi cm^2 \end{gathered}`

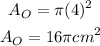
Area of the rectangle

The area of the rectangle is equal to the product of its width and length:

`A_▭=w\cdot l`

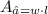
The width of the rectangle is w=2cm and the length is l=3cm, so the area can be determined as follows:

Area of the shaded region(S)

The area of the shaded area is equal to the difference between the area of the circle and the area of the rectangle:

The area of the shaded region is 44.27cm²