Question

What is the answer what is the correct answer please

Answer 1

We have to calculate the mean and standard deviation of this set of numbers.

We can calculate the mean of a set of numbers with the equation:

`\begin{gathered} M_{}=(1)/(n)\sum ^n_(i=1)\, x_i \\ M_{}=(1)/(7)(11+15+17+19+21+24+27) \\ M_{}=(134)/(7) \\ M_{}\approx19.14 \end{gathered}`

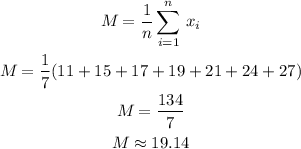
And the standard deviation can be calculated as:

`\begin{gathered} s_{}=\sqrt{(1)/(n-1)\sum_(i=1)^n\,(x_i-M_2)^2} \\ s_{}=\sqrt{(1)/(6)((11-19.14)^2+(15-19.14)^2+(17-19.14)^2+. . . +(27-19.14)^2)} \\ s_{}=\sqrt{(176.86)/(6)} \\ s=√(29.48)\approx5.43 \end{gathered}`

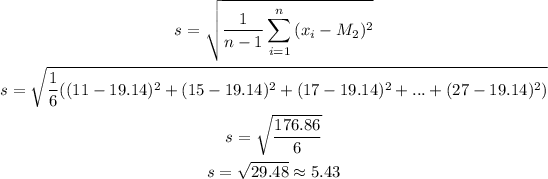
Answer:

The mean of this sample is 19.14.

The standard deviation of this sample is 5.43.