The two triangles are similar triangles. As such, the following is true:
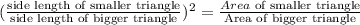
Thus, we first have to compute the area of the bigger triangle, as follows:
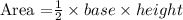
Since, for the bigger triangle, base = 81cm, and height = 36cm, we have:

Now, we find x and y, as follows:
![\begin{gathered} ((x)/(36))^2=(54)/(1458) \\ \Rightarrow((x)/(36))^2=(1)/(27) \\ \Rightarrow(x)/(36)=\sqrt[]{(1)/(27)}=\frac{1}{\sqrt[]{27}} \\ \Rightarrow(x)/(36)=\frac{1}{\sqrt[]{9*3}}=\frac{1}{\sqrt[]{9}*\sqrt[]{3}}=\frac{1}{3*\sqrt[]{3}} \\ \Rightarrow x=36*\frac{1}{3*\sqrt[]{3}}=\frac{36}{3\sqrt[]{3}}=\frac{12}{\sqrt[]{3}} \\ \Rightarrow x=\frac{12}{\sqrt[]{3}}*\frac{\sqrt[]{3}}{\sqrt[]{3}}=\frac{12\sqrt[]{3}}{\sqrt[]{9}}=\frac{12\sqrt[]{3}}{3}=4\sqrt[]{3} \\ \Rightarrow x=4\sqrt[]{3}\text{ cm} \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/rrg2blw7cjt4cd9aq9detaxbldhn5n213o.png)
Now, y can be obtained similarly:
![\begin{gathered} ((y)/(81))^2=(54)/(1458) \\ \Rightarrow((y)/(81))^2=(1)/(27) \\ \Rightarrow(y)/(81)=\sqrt[]{(1)/(27)}=\frac{1}{\sqrt[]{27}} \\ \Rightarrow(y)/(81)=\frac{1}{\sqrt[]{9*3}}=\frac{1}{\sqrt[]{9}*\sqrt[]{3}}=\frac{1}{3*\sqrt[]{3}} \\ \Rightarrow y=81*\frac{1}{3*\sqrt[]{3}}=\frac{81}{3\sqrt[]{3}}=\frac{27}{\sqrt[]{3}} \\ \Rightarrow y=\frac{27}{\sqrt[]{3}}*\frac{\sqrt[]{3}}{\sqrt[]{3}}=\frac{27\sqrt[]{3}}{\sqrt[]{9}}=\frac{27\sqrt[]{3}}{3}=9\sqrt[]{3} \\ \Rightarrow y=9\sqrt[]{3}\text{ cm} \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/2tkv6to3jo4s9gj9u4e11kjr3k2efldxxm.png)