Question

The slope of the tangent to a function f(x) at point (2,7) is mt = 3. Write the equation of the tangent line at the given point.

Answer 1

The form of the linear equation is

`y=mx+b`

m is the slope

b is the y-intercept

Since the slope of the tangent at point (2, 7) is 3, then

m = 3

Substitute it in the form of the equation above

`y=3x+b`

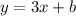
To find b,

Substitute x by 2 and y by 7 in the equation

`\begin{gathered} x=2,y=7 \\ 7=3(2)+b \\ 7=6+b \end{gathered}`

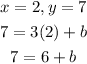
Subtract 6 from both sides

`\begin{gathered} 7-6=6-6+b \\ 1=b \end{gathered}`

The equation of the tangent is

`y=3x+1`

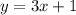
The answer is

The equation of the tangent at the point (2, 7) is y = 3x + 1