Question

A waterwheel of radius 3m is submerged such that its bottom is 2m underwater. At t=0, a boot (submerged to a depth of 2m) gets stuck in a spoke. Five seconds late the boot is at a high point. a)Find all possible times when the boot will be 2m above the water. b) Determine the length of time the boot is a bove water level.

Answer 1

We know that the waterwheel has a radius of 3 meters, this means that it has a diameter of 6 meters. Now since it is spinning we can describe its motion (and then the motion of the boot) with a cosine or sine function.

We know that in general a sinusoidal model is describe as:

`y=A\sin (B(t+C))+D`

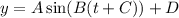
where A is the amplitude, the period is 2pi/B, C is the phase shift and D is the vertical shift.

In this case the amplitude will be 3 (since it is the radius of the wheel).

We also need that the period to be 10, this comes from the fact that it takes the boot five second to at the top, which means it will take 10 seconds to return to the bottom. From this we have:

`\begin{gathered} (2\pi)/(B)=10 \\ B=(2\pi)/(10) \\ B=(\pi)/(5) \end{gathered}`

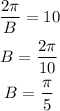
Now since we need that the motion starts at the bottom of the whell this means we need the minimum of the function to be at t=0, hence we need that the product BC to be -pi/2, then:

`\begin{gathered} BC=-(\pi)/(2) \\ C=((\pi)/(2))/((\pi)/(5)) \\ C=(5)/(2) \end{gathered}`

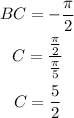
Finally we know that the wheel is two meters underwater, this means that the vertical shift to be +1.

Hence the function that describes the motion is:

`y=3\sin ((\pi)/(5)(t-(5)/(2)))+1`

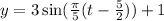
Once we have the motion describe we can answer the questions.

a)

To determine all possible times when the boot is 2 m above water we equate the expression for the height of the boot to two and solve for t:

`\begin{gathered} 3\sin ((\pi)/(5)(t-(5)/(2)))+1=2 \\ 3\sin ((\pi)/(5)(t-(5)/(2)))=1 \\ \sin ((\pi)/(5)(t-(5)/(2)))=(1)/(3) \\ (\pi)/(5)(t-(5)/(2))=\sin ^(-1)((1)/(3)) \\ (\pi)/(5)t-(\pi)/(2)=\sin ^(-1)((1)/(3)) \\ (\pi)/(5)t=(\pi)/(2)+\sin ^(-1)((1)/(3)) \\ t=(5)/(2)+(5)/(\pi)\sin ^(-1)((1)/(3)) \end{gathered}`

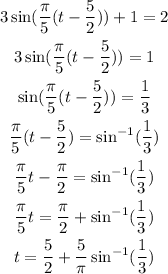
Adding the period we have:

`t=(5)/(2)+(5)/(\pi)\sin ^(-1)((1)/(3))+10n`

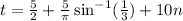
This gives the values while ascending. To find the times while it descends we use the fact that:

`\begin{gathered} 3\sin ((\pi)/(5)(t-(5)/(2)))+1=2 \\ 3\lbrack\sin ((\pi t)/(5))\cos ((\pi)/(2))-\sin ((\pi)/(2))\cos ((\pi t)/(5))\rbrack+1=2 \\ -3\cos ((\pi t)/(5))=1 \\ \cos ((\pi t)/(5))=-(1)/(3) \\ (\pi t)/(5)=\cos ^(-1)(-(1)/(3)) \\ t=(5)/(\pi)\cos ^(-1)(-(1)/(3)) \end{gathered}`

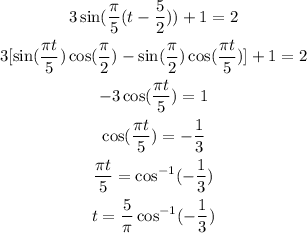
Substracting this to the period we have:

`t=10n-(5)/(\pi)\cos ^(-1)(-(1)/(3))`

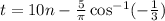
Therefore the times for which the boot will be two meters above are:

`\begin{gathered} t=(5)/(2)+(5)/(\pi)\sin ^(-1)((1)/(3))+10n \\ t=10n-(5)/(\pi)\cos ^(-1)(-(1)/(3)) \end{gathered}`

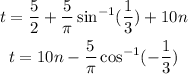
This is approximately to the times:

`t=3.03,\text{ 6.95, 13.03, 16.95,}\ldots..`

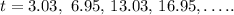
b)

The boot is above water from the time when y=0, then:

`\begin{gathered} 3\sin ((\pi)/(5)(t-(5)/(2)))+1=0 \\ \sin ((\pi)/(5)(t-(5)/(2)))=-(1)/(3) \\ (\pi)/(5)(t-(5)/(2))=\sin ^(-1)(-(1)/(3)) \\ t-(5)/(2)=(5)/(\pi)\sin ^(-1)(-(1)/(3)) \\ t=(5)/(2)+(5)/(\pi)\sin ^(-1)(-(1)/(3)) \\ t=1.959 \end{gathered}`

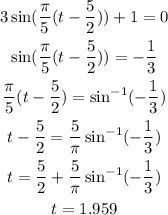
to the time when y is once again zero,

`\begin{gathered} -3\cos ((\pi t)/(5))=-1 \\ \cos ((\pi t)/(5))=(1)/(3) \\ (\pi)/(5)t=\cos ^(-1)((1)/(3)) \\ t=(5)/(\pi)\cos ^(-1)((1)/(3)) \end{gathered}`

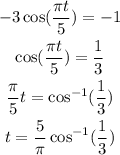
Substracting this to the period we have:

`t=10-(5)/(\pi)\cos ^(-1)((1)/(3))=8.04`

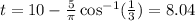
Therefore the boot is above water appoximately 6.081 seconds.