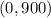Question

A rocket is launched with an initial velocity of 100ft. The height of the rocket in meters is modeled by the function shown, t is time in seconds. Write a statement that describes the domain and function and range of this function

Answer 1

• Domain: (0,30)

,

• Range: (0, 900)

Explanation:

The equation that models the height of the rocket is:

`h(t)=-4t^2+120t`

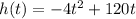
Domain

The domain of the function is the set of all the possible values of t (in seconds) for which the height is defined.

First, find the zeros of the function:

`\begin{gathered} -4t(t-30)=0 \\ -4t=0\text{ or }t-30=0 \\ t=0\text{ or }t=30 \end{gathered}`

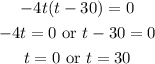
Since the height of the rocket cannot be negative, the domain of h(t) is:

`(0,30)`

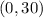
Range

The leading coefficient is negative, so the equation has an upside-down parabola.

First, we find the maximum point of the parabola by using the vertex formula.

`Vertex=(-(b)/(2a),(4ac-b^2)/(4a))`

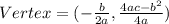
From the equation: a=-4, b=120 and c=0

Since we need just the maximum value, we calculate the y-coordinate only:

`(4ac-b^2)/(4a)=(4(-4)(0)-(120)^2)/(4(-4))=-(14400)/(-16)=900`

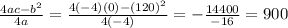
The maximum height of the rocket is 900 ft, therefore, the range of h(t) is:

`(0,900)`