Question

A certain liquid X has a normal freezing point of -6.70 °C and a freezing point depression constantK, 2.22 °C-kg-mol. A solution is prepared by dissolving some glycine (C₂H5NO₂) in 500. g of X. This solution freezesat -10.9 °C. Calculate the mass of C₂H5NO₂ that was dissolved.Round your answer to 2 significant digits.gX 5 ?

Answer 1

Step-by-step explanation

Given that:

The normal freezing point of the solvent X, T₁(solvent) = -6.70 °C

The freezing point of the solution, T₂ = -10.9 °C

The freezing point depression constant, Kf = 2.22 °C.kg/-mo

Mass of solvent X = 500.0 g = 0.50 kg

What to find:

To calculate the mass of C₂H5NO₂ that was dissolved.

Step-by-step solution:

Step 1: Calculate the freezing point depression, ΔTf.

The freezing point depression, (ΔTf) can be calculated using:

`\begin{gathered} \Delta T_f=T_1(solvent)-T_2(solution) \\ \\ \Delta T_f=-6.70^0C-(-10.9^0C) \\ \\ \Delta T_f=-6.70^0C+10.9^0C \\ \\ \Delta T_f=4.2\text{ }^0C \end{gathered}`

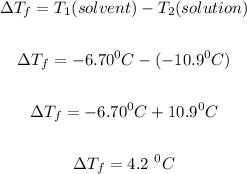
Step 2: Calculate the molal concentration of the solution.

The molality of the solution can be determined using:

`\Delta T_f=K_f* m`

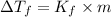
Where m is the molality of the solution.

Putting ΔTf = 4.2 °C, Kf = 2.22 °C.kg/mol, the molality of the solution is:

`\begin{gathered} 4.2^0C=2.22^0C.kg\text{/}mol* m \\ \\ m=\frac{4.2^0C}{2.22^0C.kg\text{/}mol}=1.891891892\text{ }mol\text{/}kg \end{gathered}`

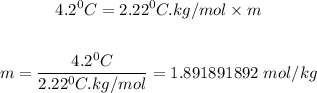
Step 3: Determine the mass of C₂H5NO₂ that was dissolved.

The mass of C₂H5NO₂ that was dissolved can be calculated using the formula for molality below:

`Molality=\frac{moles\text{ }of\text{ }solute}{kilogram\text{ }of\text{ }solvent}`

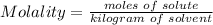
Molality = m = 1.891891892 mol/kg, kilogram of solvent = mass of X = 0.5 kg.

So,