Solution:
To graph the line that passes through two points, we first need to determine the equation of the line.
The equation of the line that passes through two points A and B is expressed as
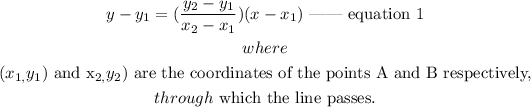
Given that the line passes through the points (1, -4) and (-2, 2), this implies

Substituting these values into equation 1, we have
![\begin{gathered} y-(-4)=((2-(-4))/(-2-1))(x-1) \\ \Rightarrow y+4=((2+4)/(-2-1))(x-1) \\ y+4=(6)/(-3)(x-1) \\ \Rightarrow y+4=-2(x-1) \\ subtract\text{ 4 from both sides of the equation} \\ y+4-4=-2(x-1)-4 \\ \Rightarrow y=-2(x-1)-4 \\ open\text{ parentheses} \\ y=-2x+2-4 \\ \Rightarrow y=-2x-2 \end{gathered}]()
Thus, the equation of the line that passes through the points (1, -4) and (-2, 2) is
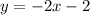
To graph the line,
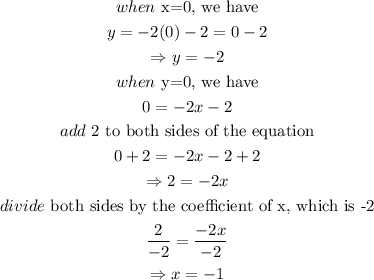
Given the points (1, -4), (-2, 2), (0,-2) and (-1,0), the graph of the line is as shown below: