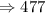Question

Find the 67th term of the following arithmetic sequence.15, 22, 29, 36,

Answer 1

The arithmetic sequence is given below as

`15,22,29,36`

Step 1:

Calculate the common difference

`\begin{gathered} d=t_2-t_1 \\ d=22-15 \\ d=7 \end{gathered}`

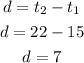
Step 2:

The nth term of an arithmetic progression is given below as

`\begin{gathered} T_n=a+(n-1)d \\ where, \\ a=15 \\ n=67 \\ d=7 \end{gathered}`

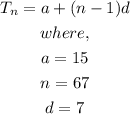
By substituting the values, we will have

`\begin{gathered} T_(67)=15+(67-1)7 \\ T_(67)=15+66*7 \\ T_(67)=15+463 \\ T_(67)=477 \end{gathered}`

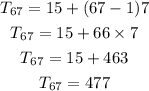
Hence,

The 67th term of the arithmetic sequence is

`\Rightarrow477`