Question

3/13/22, 9:17 PM 57069.jpeg UNIT 3 Project John makes DVDs of his friend's shows. He has realized that, because of his fixed costs, his average cost per DVD depends on the number of DVDs he produces. The cost of producing x DVDs is given by C(x) = (2500 + 1.5x if x < 1,000 (2500 + 1.25x if x > 1,000 1. John wants to figure out how much to charge his friend for the DVDs without making a profit. How much should he charge for 100 DVDs in order to break even? What is the cost per DVD? 2. Suppose John makes more than 100 DVDs for his friend. complete the table below showing his costs at different levels of production. Show all of your work. # of DVDs 0 10 100 1,000 10,000 100,000 1,000,000 Total Cost Cost per DVD 10

Answer 1

1. $2650, $26.5 per DVD

2.

Explanation:

We have that the cost of the DVD is given by a function per part, for when there are 1000 or fewer units or when there are more than 1000. Just like this:

`C(x)=\begin{cases}2500+1.5x,\text{ if x }\leq1000 \\ 2500+1.25x,\text{ if x }>1000\end{cases}`

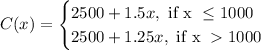
1.

Now in this case we are going to produce 100 DVDs so we use the first equation, just like this:

`\begin{gathered} C(100)=2500+1.5\cdot100 \\ C(100)=2500+150 \\ C(100)=2650 \end{gathered}`

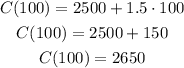
Now, since he does not want to make a profit, he must charge the same value as the cost, in order to reach the break-even point, which means that he must charge the friend $2650

The cost per DVD is calculated by dividing the total cost by the number of DVDs, just like this

`\begin{gathered} c=(2650)/(100) \\ c=26.5 \end{gathered}`

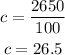
Which means the cost is $26.5 per DVD

2.

We calculate for each case:

`\begin{gathered} C(0)=0 \\ c=x \\ \\ C(10)=2500+1.5\cdot10=2515 \\ c=(2515)/(10)=251.5 \\ \\ C(100)=2500+1.5\cdot100=2650 \\ c=(2650)/(100)=26.5 \\ \\ C(1000)=2500+1.5\cdot100=4000 \\ c=(4000)/(1000)=4 \\ \\ C(10000)=2500+1.25\cdot10000=15000 \\ c=(15000)/(10000)=1.5 \\ \\ C(100000)=2500+1.25\cdot100000=127500 \\ c=(127500)/(100000)=1.275 \\ \\ C(1000000)=2500+1.25\cdot1000000=1252500 \\ c=(1252500)/(1000000)=1.2525 \end{gathered}`

We replace each value in the table and we would be left with: