Solution:
Given the infinite geometric series below
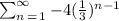
a) For the first four terms, n = 1, 2, 3, 4
Where, n = 1,
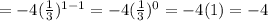
Where, n = 2
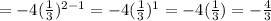
Where, n = 3
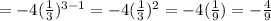
Where, n = 4
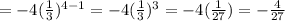
Hence, the first four terms are
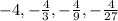
b) To confirm if the series converges or diverges,
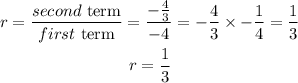
Since, the common ratio, r is between -1 and 1,
Hence, the series converges
c) To find the sum of the series, we will apply the sum to infinity formula, which is
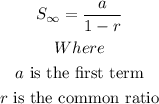
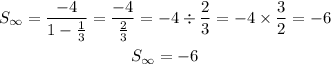
Hence, the sum is -6