Answer:
![undefined]()
Step-by-step explanation:
Let x represent the length of the third side of the given triangle.
We can go ahead and determine the value of x using the Pythagorean theorem as seen below;
![\begin{gathered} 41^2=x^2+40^2 \\ 1681=x^2+1600 \\ x^2=1681-1600 \\ x^2=81 \\ x=\sqrt[]{81} \\ x=9 \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/high-school/2uih1xm1gkaj3gfjt2o9rc94ivufvp0d60.png)
So the length of the third side of the triangle is 9
We can now determine the value of sine theta as seen below;
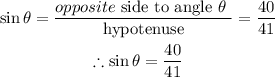
We can see that sine theta is 40/41
Let's determine the value of cosine theta as seen below;
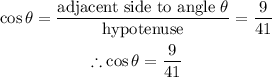
So cosine theta is 9/41
Let's determine the value of tangent theta as seen below;
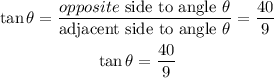
So tangent theta is 40/9
Let's now determine the value of cosecant theta as seen below;
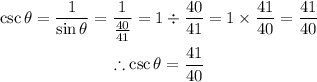
So the value of cosecant theta is 41/40
Let's determine the value of secant theta as seen below;
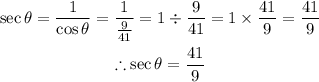
So the value of secant theta is 41/9
Let's determine the value of cotangent theta as seen below;
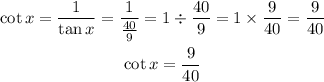
So the value of cotangent theta is 9/40