Question

For the line of fit h=0.6t+0.44 , what is the residual of the data plot at t=11 ?

Answer 1

The residual is the difference between the actual value and the predicted value.

The actual value of height at t = 11 is 7 (from the table)

The predicted value can be found using the equation of the line of best fit.

`h=0.6t+0.44`

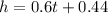
Substitute t = 11 into the above equation

`\begin{gathered} h=0.6(11)+0.44 \\ h=6.6+0.44 \\ h=7.04 \end{gathered}`

So, the residual is

`\begin{gathered} residual=actual-predicted \\ residual=7-7.04 \\ residual=-0.04 \end{gathered}`

Therefore, the residual of the data plot at t = 11 is -0.04