Question

The speed of transverse waves along a car antenna is 25.5 meters per second. The antenna is 0.681 meters tall, with one end attached to the car and the other end free to vibrate. What are the first three natural frequencies of the antenna? Include units in your answers.

Answer 1

The n-th natural frequency for a medium with length L fixed at one end and free at the other end is given by the condition:

`L=(2n-1)/(4)\lambda_n`

Where λ_n is the n-th natural wavelength. On the other hand, every transverse wave satisfies the following:

`v=\lambda f`

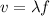
Where v is the speed of the wave, and f is the frequency of the wave.

Then:

`f_n=(v)/(\lambda_n)`

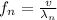
Isolate 1/λ_n from the first equation:

`(1)/(\lambda_n)=(2n-1)/(4L)`

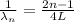
Then:

`f_n=(2n-1)/(4L)* v`

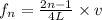
Replace L=0.681m, v=25.5m and n=1,2,3 to fin the first three natural frequencies of the antenna:

`\begin{gathered} f_1=(2(1)-1)/(4*(0.681m))*25.5(m)/(s)\approx9.36Hz \\ \\ f_2=(2(2)-1)/(4*(0.681m))*25.5(m)/(s)\approx28.1Hz \\ \\ f_3=(2(3)-1)/(4*(0.681m))*25.5(m)/(s)\approx46.8Hz \end{gathered}`

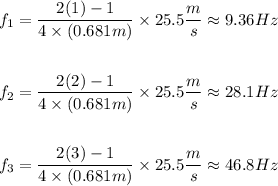
Therefore, the first three natural frequencies of the antenna are 9.36Hz, 28.1Hz and 46.8Hz.