1 Answer

Gokulakrishnan · Answer 1 · 2023-06-15T11:19:31+0000

Recall that a translation of n units to the left transforms the point (x,y) as follows:

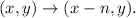
$(x,y)\rightarrow(x-n,y).$

A vertical translation of n units up transforms the point as follows:

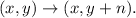
$(x,y)\rightarrow(x,y+n).$

Therefore, a point (x,y) translated 5 units to the left, and 3 units up is transformed as follows:

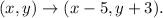
$(x,y)\rightarrow(x-5,y+3).$

Now, the coordinates of point P are:

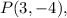
therefore, the image of point P under the transformations is:

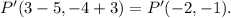
$P^(\prime)(3-5,-4+3)=P^(\prime)(-2,-1).$

Answer: