Answer:
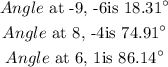
Step-by-step explanation:
Given:
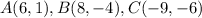
To find:
The interior angles of the triangle using vectors
If we draw this triangle using the given vertices, we'll have;
To find the angle at C(-9, -6) we need to get the vector name for vectors CA and CB as seen below;
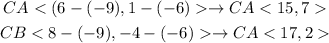
Then we'll the below formula to solve for the angle at C;

So the angle at (-9, -6) is 18.31 degrees
To find the angle at B(8, -4) we need to get the vector name for vectors BA and BC as seen below;
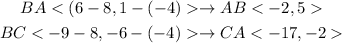
Then we'll the below formula to solve for the angle at B;

![\begin{gathered} We^(\prime)ll\text{ go ahead and determine the angle at A\lparen6, 1\rparen by first finding the vector names for } \\ vectors\text{ AB and AC;} \\ AB<8-6,-4-1>\rightarrow AB<2,-5> \\ AC<-9-6,-6-1>\rightarrow AC<-15,-7> \\ \cos(\theta)=\frac{AB\cdot AC}{Magn\imaginaryI tude\text{ of AB and AC}} \\ \cos\theta=\frac{-30+35}{\sqrt{2^2+(-5^()2)}*√((-15)^2+(-7)^2)} \\ \cos\theta=(6)/(√(29)*√(274)) \\ \cos\theta=(6)/(89.14) \\ \cos\theta=0.0673 \\ \theta=\cos^(-1)(0.0673) \\ \theta=86.1^(\circ) \\ So\text{ the angle at \lparen6, 1\rparen is 86.14 degrees} \end{gathered}]()