Question

For what value of k are the lines kx - 4y-4=0 and 3x +(k-1)y - 3 =0 perpendicular lines? Write the equation of both lines and sketch the graph of both

Answer 1

We have the lines

`\begin{gathered} kx-4y-4=0\text{ } \\ \text{and} \\ 3x+(k-1)y-3=0 \end{gathered}`

and we would like to know for which value of k the lines are perpendicular. To do this we first write the lines in the slope intercept form:

`y=mx+b`

that is, we solve the equations for y. We are going to do that so that we can see what the slope in each equation is.

For the first equation we have

`\begin{gathered} kx-4y-4=0 \\ kx-4=4y \\ y=(k)/(4)x-(4)/(4) \\ y=(k)/(4)x-1 \end{gathered}`

then, in the first line the slope is k/4.

For the second equation we have

`\begin{gathered} 3x+(k-1)y-3=0 \\ (k-1)y=-3x+3 \\ y=-(3)/(k-1)x+(3)/(k-1) \end{gathered}`

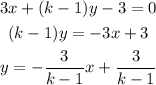
then the slope for the second equation is -3/(k-1).

Now that we have the both slopes, we have to remember that two lines will be perpendicular if and only if their slopes fulfill:

`m_1m_2=-1`

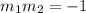
Plugging our values for the slopes we have

`((k)/(4))(-(3)/(k-1))=-1`

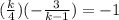
Now that we have our equation for k we only have to solve it so let's do that,

`\begin{gathered} ((k)/(4))(-(3)/(k-1))=-1 \\ (-3k)/(4(k-1))=-1 \\ -3k=-1(4(k-1)) \\ -3k=-4(k-1) \\ -3k=-4k+4 \\ 4k-3k=4 \\ k=4 \end{gathered}`

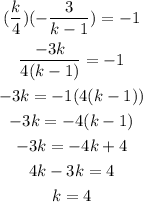
Therefore the lines will be perpendicular if k=4.

For this value of k the equations will take the form :

`\begin{gathered} kx-4y-4=0\rightarrow4x-4y-4=0 \\ \text{and} \\ 3x+(k-1)y-3=0\rightarrow3x+3y-3=0 \end{gathered}`

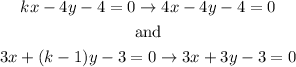
So the equations will be 4x-4y-4=0 and 3x+3y-3=0.

If we graph both eqautions we see that they are perpendicular to each other, like we wanted.

Where the red line is 4x-4y-4=0 and the blue line is 3x+3y-3=0.