Question

A chemist needs to make 3 mL of a 10% methane solution from a 6% methane solution and a 40% methane solution.

If we let x be the number of mL of the 6% methane solution and y be the number of mL of the 40% methane
solution, how would you set up two equations using x and y to find how many mL of each solution the chemist
needs to mix to get the desired solution ?

Answer 1

Given:

A chemist needs to make 3 mL of a 10% methane solution from a 6% methane solution and a 40% methane solution

Aim:

We need to find equations to find the number of ml of each solution.

Step-by-step explanation:

Let x be the number of mL of the 6% methane solution and y be the number of mL of the 40% methane

We know that the total number of ml of the 10% solution is 3ml.

The number of mL of the 6% methane solution + the number of mL of the 40% methane = the total number of ml of the 10% solution

`x+y=3`
`6\text{ \% of x+40 6 of y =10 \% of 3}`

`(6)/(100)x+\frac{\text{40}}{100}\text{y =}(10)/(100)*3`

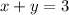
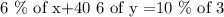
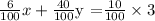
Multiply both sides by 100.

`100*(6)/(100)x+100*\frac{\text{40}}{100}\text{y =100}*(10)/(100)*3`

`6x+40y=10*3`

`6x+40y=30`

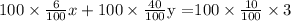
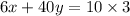
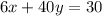
The required two equations are

`x+y=3`

`6x+40y=30`

`Consider\text{ the equation }x+y=3.`
`x=3-y`

`Substitute\text{ x=3-y in the equation }6x+40y=30.`
`6(y-3)+40y=30`

`6y-6*3+40y=30`

`6y-18+40y=30`

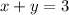
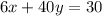
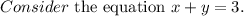
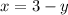
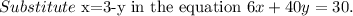
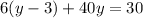
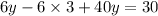
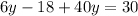
Solve for y.

`6y+40y=30+18`

`46y=48`
`y=(48)/(46)`
`y=(24)/(23)`
`y=1.04ml`

`Substitute\text{ }y=(24)/(23)\text{ in the equation x=3-y.}`
`x=3-(24)/(23)`

`x=(3*23)/(23)-(24)/(23)`

`x=(69)/(23)-(24)/(23)`

`x=(69-24)/(23)`

`x=(45)/(23)`
`x=1.96ml`

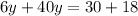
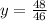
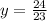
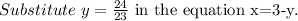
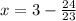
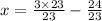
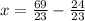
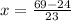
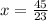
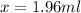
Final answer:

The equations:

`x+y=3`
`6x+40y=30`

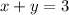
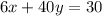
The number of mL of the 6% methane solution is 1.04 ml.

The number of mL of the 40% methane solution is 1.96 ml.