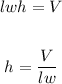ANSWER:
V/(lw)
Explanation:
We have the following equation:
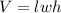
To solve for a variable, what we must do is that the variable remains alone to a quantity or unknown in one of the members of an equality (generally shown on the left)
The indicated variable is h, therefore: