Question

Solve the equation completing the square in vertex form. y=3x^2-12x+17

Answer 1

`y=3(x-2)^2+5`

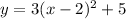
Step-by-step explanation

We want to put the equation given in vertex form:

`y=3x^2-12x+17`

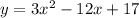
The vertex form of a quadratic equation is:

`y=a(x-h)^2+k`

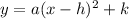
The first step is to subtract 17 from both sides of the equation:

`\begin{gathered} y-17=3x^2-12x+17-17 \\ y-17=3x^2-12x \end{gathered}`

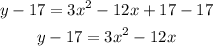
The next step is to complete the square of the expression on the right-hand side:

`\begin{gathered} y-17=3(x^2-4x) \\ \Rightarrow y-17+12=3(x^2-4x+4) \end{gathered}`

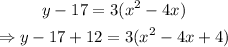
Note: 12 is added to the left side of the equation because it was added to the right side to complete the square.

Now, factorize the right-hand side:

`\begin{gathered} y-5=3(x^2-2x-2x+4) \\ y-5=3\lbrack(x-2)(x-2)\rbrack \\ y-5=3(x-2)^2 \end{gathered}`

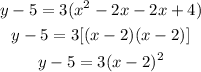
Finally, add 5 to both sides of the equation:

`\begin{gathered} y-5+5=3(x-2)^2+5 \\ y=3(x-2)^2+5 \end{gathered}`

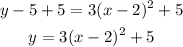
That is the vertex form of the equation.