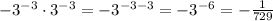Hello there. To solve this question, we'll need some properties from powers:
First, something to the 0-th power is equal to 1:
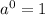
Second, multiplying powers of the same base is equal to keeping the base and adding the powers:
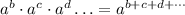
Third, dividing powers of the same base is equal to keeping the base and subtracting the powers:
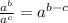
For the first question.
(-3^(-2))^0, applying the first rule, it will be equal to 1.
For the second question, keeping the base and adding the powers, we have:
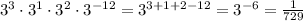
For the third question, keeping the base and subtracting the powers, we have:
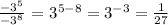
Finally, for the fourth question, keeping the base and adding the powers, we have: