In this type of question, for us to be able to get the coordinates of the triangle's circumcenter, the following are the steps that we are going to do.
Step 1: Determine the coordinates of at least two midpoints of the triangle.
Step 2: Generate the formula of the 2 bisecting lines (from vertex to midpoint)
Step 3: Equating the equations of two bisecting lines to find their point of intersection which is also the triangle's circumcenter.
We get,
Step 1: Determine the coordinates of at least two midpoints of the triangle.
Midpoint between P and Q,
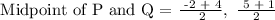
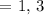
Midpoint between Q and R,
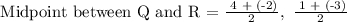
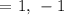
Step 2: Generate the formula of the 2 bisecting lines (from vertex to midpoint).
Equation 1: Midpoint P & Q to Vertex R.
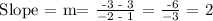
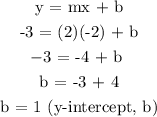
The equation is, therefore,
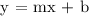
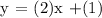
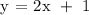
Equation 2: Midpoint Q and R to vertex P.
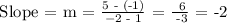
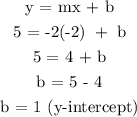
The equation is, therefore,
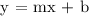
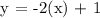
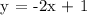
Step 3: Equating the equations of two bisecting lines to find their point of intersection which is also the triangle's circumcenter.
Using the substitution method,
y = 2x + 1
y = -2x + 1
2x + 1 = -2x + 1
2x + 2x = 1 - 1
4x = 0
4x/4 = 0/4
x = 0
At x = 0,
y = 2(0) + 1
y = 1
Therefore, the coordinate of the circumcenter of the triangle PQR is 0, 1
Plotting the triangle will be,