We must transform triangle ABC.
In part (a) the transformation that we must apply is:
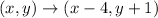
Now we take the three points A, B and C and we apply the transformation to them. The resulting points will be the vertices of triangle T. Then we get:
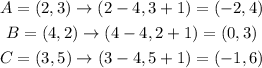
Then triangle T and the answer to part a is:
In part b we must use this transformation:
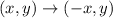
We apply this transformation to A, B and C:
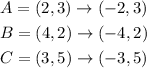
Then triangle R and answer to part b is: