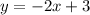Given:
The given points are A(-3,-1) and B(5,3).
Required:
We need to find the set of all points that are the same distance from the points A(-3,-1) and B(5,3).
Step-by-step explanation:
Recall that the set of points that are the same distance from the point A(-3,-1) and (5,3) is the perpendicular bisector of the line segment AB.
Consider the slope formula.
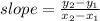

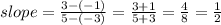
We get the slope of the line segment AB is 1/2.
The slope of the perpendicular is the negative reciprocal of the slope of the line segment AB.
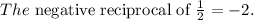

The perpendicular line is passing through the midpoint of A(-3,-1) and B(5,3).
Consider the midpoint formula.
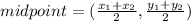
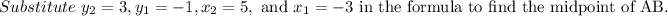
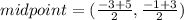
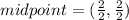
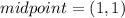
Consider the general form of the line equation.

Substitute m=-2, x=1, and y=1 in the line equation to find b.
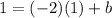
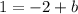
Add 2 to both sides of the equation.
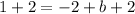
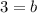
Substitute m=-2 and b=3 in the line equation.
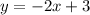
We get the perbenticular bisector y =-2x+3.
Final answer: