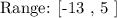Question

Given the function f(x)=3x-1, what is the range when the domain is {-4,0,1,2}?

Answer 1

We will investigate how to evaluate the range of a function given the domain.

A function is defined as a algebraic expression that relates an independent variable like ( x ) and a dependent variable like ( y ). A unique relationship is established between the two variables using a set of operator(s). A function f ( x ) is given in the problem statement as follows:

`f\text{ ( x ) = 3x - 1}`

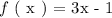
A domain of a function defines a list of values associated with the independent variable like ( x ). This set of values controls the output of the function given. The set of domain is expressed as follows:

`\text{Domain: x }\in\mleft\lbrace\text{ -4 , 0 , 1 , 2 }\mright\rbrace`

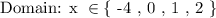
A range of the function is an interval within which the output of the function lies defined by the relationship i.e function and the set of domain values. These values are the output values of the dependent variable. The interval is only defined by the maximum and minimum attained value of the dependent variable ( y ) for the entire list of domain values. The range is usually expressed as:

`\text{Range: \lbrack a , b \rbrack}`

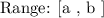
Where,

To determine the above two values we will evaluate the given function f ( x ) for each value of the domain. We will plug in or replace the independent variable ( x ) in the function relationship for each value of the domain and have a set of output values as follows:

`\begin{gathered} x\text{ = -4,} \\ f\text{ ( -4 ) = 3}\cdot(-4)\text{ - 1 = -13} \\ \\ x\text{ = 0,} \\ f\text{ ( 0 ) = 3}\cdot(0)\text{ - 1 = -1} \\ \\ x\text{ = 1 ,} \\ f\text{ ( 1 ) = 3}\cdot(1)\text{ - 1 = 2} \\ \\ x\text{ = 2,} \\ f\text{ ( 2 ) = 3}\cdot(2)\text{ - 1 = 5} \end{gathered}`

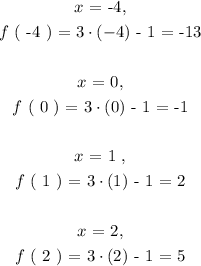
We will compile the list of output values for each corresponding value of domain.

From the list compiled above we can pluck out the maximum and minimum value attained by the dependent varaible ( y ) over the entire domain.

`\begin{gathered} \text{Minimum ( a ) = -13} \\ \text{Maximum ( b ) = 5} \end{gathered}`

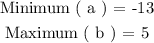
Therefore, the range of the function is:

`\text{Range: \lbrack -13 , 5 \rbrack}`