The free-body diagram of the given situation is shown below:
Fr is the friction force, N is the normal force, Mgcosθ and Mgsinθ are the components of the weight for the case of a body on an incline.
The friction force is given by:
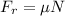
Due to the system is in equilibrium for the forces perpendicular to the plane, you have:

Then, for Fr:

where,
θ: angle of the incline = 40
M: mass of the body = 10 kg
g: gravitational acceleration constant = 9.8 m/s^2
Replac