Question

Given the function f(x)= 6x^2+4x-1. Calculate the following values: F(0)=F(2)=F(-2)=F(x+1)=F(-x)=

Answer 1

Given,

The expression is,

`f(x)=6x^2+4x-1`

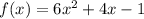
Substituting x = 0,

`f(0)=6(0)^2+4(0)-1=-1`

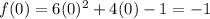
The value of f(0) is -1.

Substituting x = 2,

`f(2)=6(2)^2+4(2)-1=31`

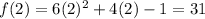
The value of f(2) is 31.

Substituting x = -2,

`f(-2)=6(-2)^2+4(-2)-1=15`

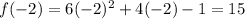
The value of f(-2) is 15.

Substituting x = x+1,

`\begin{gathered} f(x+1)=6(x+1)^2+4(x+1)-1 \\ =6(x^2+1+2x)+4x+4-1 \\ =6x^2+6+12x+4x+3 \\ =6x^2+16x+9 \end{gathered}`

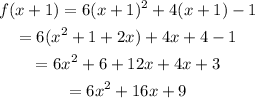
The value of f(x+1) is 6x^2+16x+9.

Substituting x = -x,

`\begin{gathered} f(-x)=6(-x)^2+4(-x)-1 \\ =6(x^2)-4x-1 \\ =6x^2-4x-1 \end{gathered}`

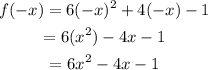
The value of f(-x) is 6x^2-4x-1.