Given:
The probability that a randomly selected worker primarily drives a bicycle to work is,
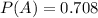
The probability that a randomly selected worker takes public transportation is,
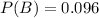
Step-by-step explanation:
a) To find: The probability that a randomly selected worker primarily drives a bicycle or public transportation to work
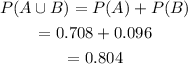
Thus, the answer is 0.804.
b) To find: The probability that a randomly selected worker primarily drives neither a bicycle nor public transportation to work
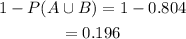
Thus, the answer is 0.196.
c) To find: The probability that a randomly selected worker does not drive a bicycle to work
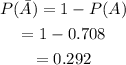
Thus, the answer is 0.292.
d) To check: The probability that a randomly selected worker walks to work is 0.30.
We know that the total probability is 1.
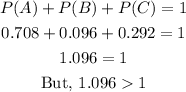
So, the answer is,
No, the probability a worker primarily drives a bicycle, walks, or public transportation would be greater than 1.