Question

4. Find the perimeter and the area of the triangle in the graphbelow.

Answer 1

To find the area and the perimeter for a right triangle, first, we need to calculate the values for the two legs and the hypotenuse. To do so, we will use the following definition for a distance of two points:

`d_(a-b)=\sqrt[]{(x_a-x_b)^2+(y_a-y_b)^2}`

Applying this for the present question, we have:

`\begin{gathered} d_(AB)=\sqrt[]{(-2-3)^2+(-4-8)^2}=\sqrt[]{(-5)^2+(-12)^2}=\sqrt[]{25+144} \\ d_(AB)=\sqrt[]{169}=13 \\ \\ d_(BC)=\sqrt[]{(3-3)^2+(-4-8)^2}=\sqrt[]{(0)^2+(-12)^2}=\sqrt[]{144} \\ d_(BC)=12_{} \\ \\ d_(AC)=\sqrt[]{(-2-3)^2+(-4-(-4))^2}=\sqrt[]{(-5)^2+(0)^2}=\sqrt[]{25} \\ d_(AC)=5 \end{gathered}`

Now, we know that the perimeter of a triangle is just the sum of each side, as follows:

`P_{\text{ABC}}=5+12+13=30\text{ }u`

And the area of a right triangle is given by half of the multiplication of the legs, as follows:

`A_(ABC)=(d_(BC)* d_(AB))/(2)=(12*5)/(2)=(60)/(2)=30\text{ }u^2`

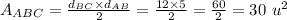
Where u stands for an arbitrary unit.