Question

Solve the system of equations using substitution 2x+4y=7x=-2y+7

Answer 1

Step-by-step explanation

`\begin{gathered} 2x+4y=7\Rightarrow equation(1) \\ x=-2y+7\Rightarrow equation(2) \end{gathered}`

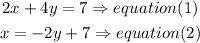
this method works by solving one of the equations , for one of the variables, and then plugging this back into the other equation, "substituting" for the chosen variable and solving for the other

Step 1

we can see that in equation (2) x is isolated, so we just need to replace this value in equation(1)

so

when we got an indetermination, it means the system HAS NOT SOLUTiON

I hope this helps you