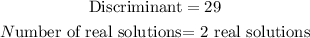Question

Compute the value of the discriminant and give the number of real solutions of the quadratic equation.5x² - 7x+1=0Discriminant:Number of real solutions:

Answer 1

The formula for the discriminant (D) of a quadratic equation is,

`D=b^2-4ac`

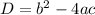
The given quadratic equation is,

`5x^2-7x+1=0`

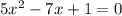
The general formula for quadratic equation is,

`ax^2+bx+c=0`

Comparing the general quadratic formula with the quadratic equation given, we have

`\begin{gathered} a=5 \\ b=-7 \\ c=1 \end{gathered}`

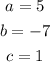
Solving for the discriminant

`\begin{gathered} D=(-7)^2-4(5)(1)=49-20=29 \\ \therefore D=29 \end{gathered}`

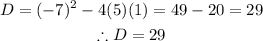
Hence, the discriminant of the quadratic equation(D) is 29.

Let us now solve for the number of real solutions

Since D > 0,

Hence, the quadratic equation has 2 real solutions.

The graph of the quadractic equation will be shown below

Finally,

`\begin{gathered} \text{Discriminant}=29 \\ N\text{umber of real solutions= 2 real solutions} \end{gathered}`