the line is perpendicular to the line:
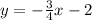
this means that the slope of the line will be the negative reciproc of the other line so it would be:
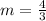
now with the slope and the coordinate (3,8) we can find the intersection with the y axis by replacing x = 0 so
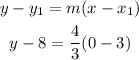
and we solve for y
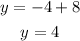
So finally we can write the general equation like:
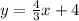
where m = 4/3 and c = 4