Question

It took a group of students 5 hours to drive to the beach for Spring Break. On the return home, due to traffic, it took the group 6.5 hours to return home. Their speed was 15 mi/hr slower on their trip home than on drive to the beach. What was their speed on the return trip home?

Answer 1

50 mi/hr.

Explanation:

`\begin{gathered} Speed=(Distance)/(Time) \\ \implies Distance=Speed* Time \end{gathered}`

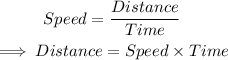
Let the speed on the way to the beach = x mi/hr

The time it took to drive to the beach = 5 hours

`Distance\;covered=5x`

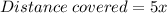
On their trip home, their speed was 15 mi/hr slower.

• Speed = (x-15) mi/hr

The time it took to drive back home = 6.5 hours

`Distance\;covered=6.5(x-15)`

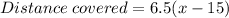
Since the distance to and from the beach is the same, then:

`5x=6.5(x-15)`

We solve the equation for x:

Thus, the speed on the return home will be:

`x-15=65-15=50\text{ mi/hr}`

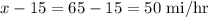
Their speed on the return trip home was 50 mi/hr.