Question

|4x-8| =8 the equation has two solution find the sum if those two solution.

Answer 1

This problem has an absolute value operator, this type of math operator receives a number as an input and outputs a positive value. This means that if we have an equation like "|x| = 3" it will have two possible solutions, because if x = -3 the result will be true and if x = 3 the result will also be true.

With this in mind let's solve the problem.

`\begin{gathered} |4x\text = 8 \\ \end{gathered}`

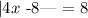
We need to create two equations. The first one is for the case where "4x -8" is greater than 0 and the second one if "4x -8" is less then 0.

For the first case we have:

`\begin{gathered} 4x\text{ -8 = }8 \\ 4x\text{ = 8 + 8} \\ 4x\text{ = 16} \\ x=(16)/(4)\text{ =4} \end{gathered}`

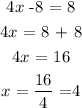
For the second case we have:

`\begin{gathered} 4x\text{ - 8 = -8} \\ 4x\text{ = -8 +8} \\ 4x\text{ = 0} \\ x\text{ = 0} \end{gathered}`

Therefore the two solutions are x = 0 and x = 4 and their sum is:

`0+4\text{ = 4}`

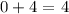
The answer to the problem is 4.