Since ∆JKL and ∆MNO are similar, this means, the ratio of each corresponding sides is equal.
Therefore, we can say that:
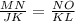
Let's plug in the length of MN, JK, and NO in the equation above.
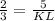
Then, solve for KL.

Therefore, the length of side KL is 7.5 units.