Question

Pls help: without graphing determine whether the function represents exponential growth or exponential decay. Then find y-intercept

Answer 1

Given

`0.99((1)/(3))^x`

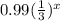
To determine whether the function represents exponential growth or exponential decay, and the y-intercept.

now,

It is given that,

`0.99((1)/(3))^x`

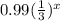
The exponential functions are of the form,

`y=ab^x`

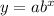
If a is positive and b is greater than 1, then it represents exponential growth.

And, if a is positive and b is greater than 0 and less than 1, then it represents exponential decay.

Since b=1/3<1.

Then, the given function represents exponential decay.

The y- intercept of the function is,

`\begin{gathered} y=0.99((1)/(3))^x \\ \text{When x=0.} \\ y=0.99((1)/(3))^0 \\ y=0.99 \end{gathered}`

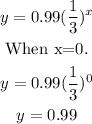
Hence, the y-intercept is 0.99.