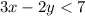Question

Hello, I need help on two variable linear equations:Which inequality matches the graph?

Answer 1

We must find the inequality that represents the points in the shaded region of the plane. From the graph, we see that the points are strictly over a line. Let's find the equation of the dotted line.

We see that the line passes through the points:

• P1 = (x1,y1) = (5,4),

,

• P2 = (x2,y2) = (3,1).

The slope of the line is:

`m=(y_2-y_1)/(x_2-x_1)=(1-4)/(3-5)=(-3)/(-2)=(3)/(2)\text{.}`

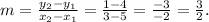
The point-slope equation of the line is:

`\begin{gathered} y=m\cdot(x-x_1)+y_1, \\ y=(3)/(2)\cdot(x-5)+4=(3)/(2)\cdot x-(15)/(2)+4=(3)/(2)\cdot x-(7)/(2). \end{gathered}`

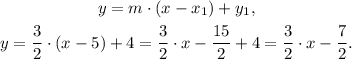
As we said above, the points are over the dotted line, so we have the following inequality:

`\begin{gathered} y>(3)/(2)x-(7)/(2), \\ 2y>3x-7, \\ 7>3x-2y. \end{gathered}`

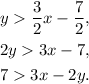
Or:

`3x-2y<7`

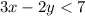
Answer

Last option:

`3x-2y<7`