Question

Solve the 5 questions. I beg you T_T (90 points!!!)

Answer 1

8) Consistent and Dependent

`\boxed{\begin{aligned}3x-3y&=6\\-x+y&=-2\end{aligned}}`

9) Consistent and Independent

`\boxed{\begin{aligned}x+y&=0\\-x+y&=-8\end{aligned}}`

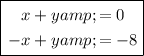
10) Inconsistent

`\boxed{\begin{aligned}4x&+2y=6\\4y&=-8x+4\end{aligned}}`

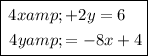
11) Solution: (3, 0)

12) Solution: (-2, 1)

Explanation:

System of equations

• A consistent and dependent system has infinitely many solutions. When graphed, the equations will result in overlapping lines, forming a single line.
• A consistent and independent system has a unique solution. When graphed, the equations will result in two lines that intersect at a single point.
• An inconsistent system has no solution. When graphed, the equations will result in two parallel lines that never intersect.

`\hrulefill`

Question 8

The graph shows a single line, so the system is consistent and dependent.

Find the equation of the line by calculating its slope (m) and y-intercept (b), and then inputting these into the slope-intercept formula, y = mx + b.

The line passes through the points (0, -2) and (2, 0).

Input these points into the slope formula to calculate the slope of the line:

`\textsf{Slope ($m$)}=(y_2-y_1)/(x_2-x_1)=(0-(-2))/(2-0)=(2)/(2)=1`

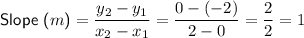
The y-intercept is b = -2.

Therefore, the slope-intercept equation of the line is:

`y=x-2`

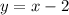
Rearrange this by subtracting x from both sides:

`-x+y=-2`

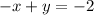
Therefore, the correct set of equations for the given system is:

`\boxed{\begin{aligned}3x-3y&=6\\-x+y&=-2\end{aligned}}`

`\hrulefill`

Question 9

The graph shows two lines that intersect at a single point, so the system is consistent and independent.

One of the lines passes through the origin (0, 0).

The only set of equations where y = 0 when x = 0 is the set with the equation x + y = 0.

Therefore, the correct set of equations for the given system is:

`\boxed{\begin{aligned}x+y&=0\\-x+y&=-8\end{aligned}}`

`\hrulefill`

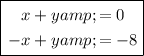
Question 10

The graph shows two parallel lines, so the system is inconsistent .

Find the equation of one of the lines by calculating its slope (m) and y-intercept (b), and then inputting these into the slope-intercept formula, y = mx + b.

The first line passes through the points (0, 1) and (0.5, 0).

Input these points into the slope formula to calculate the slope of the line:

`\textsf{Slope ($m$)}=(y_2-y_1)/(x_2-x_1)=(1-0)/(0-0.5)=-2`

The y-intercept is b = 1.

Therefore, the slope-intercept equation of the line is:

`y=-2x+1`

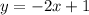
Multiply all terms by 4:

`4y=-8x+4`

Therefore, the correct set of equations for the given system is:

`\boxed{\begin{aligned}4x&+2y=6\\4y&=-8x+4\end{aligned}}`

`\hrulefill`

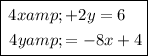
Question 11

The solution to the graphed consistent and independent system is the point where the two lines intersect.

From observation of the given graph, the point of intersection of the two lines is (3, 0).

`\hrulefill`

Question 12

The solution to the graphed consistent and independent system is the point where the two lines intersect.

From observation of the given graph, the point of intersection of the two lines is (-2, 1).