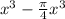From the question,
The formula for the volume(V1) of the cube is,
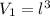
Given that:
The length of the cube is x
Therefore,
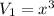
The formula for the volume (V2) of the cylinder is,
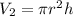
Given:
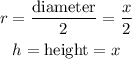
Therefore,
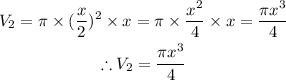
Hence, the volume(V) of water that can be poured inside the rectangular prism yet outside the cylinder will be
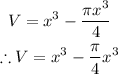
Therefore, the expression that will help Cole solve for the volume is,