Given the function:
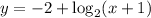
To compare the graphs, follow the steps below.
Step 1: Choose a value for x in order to evaluate the graphs.
Let's choose x = 0.
Then, substituting x by 0 in the equation:
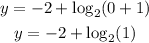
Step 2: Solve the equation above.
Knowing that log₂(1) is 0:
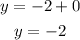
So, the graph must have the point (0, -2).
Step 3: Find the point (0, -2) in the graphs.
Comparing the graphs, we can observe that only the graph drawn by Stephen contains the point (0, -2).
Answer: Stephen.