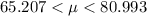Here we basically need to fin a confidence interval using the formula:
![\mu\pm z\cdot\frac{S}{\sqrt[]{n}}](https://img.qammunity.org/2023/formulas/mathematics/college/kz1bde0ifottt08ma7jplmmg7nk7cni9kk.png)
Where μ is the mean if the sample, S is the standard deviation, n is the size and z is known as the z-value and is related to the fact that we are assuming the data is from a normally distributed population. The questions gives us the following values: μ=73.1 S=16.5 and n=29. In order to find z we need the value of n and something known as the significance level that is given by:
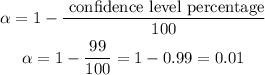
Knowing that the sizes of the sample is 29 and the significance level is 0.01 we can find z in a table or using a calculator: z=2.576. Then we can find the confidence interval:
![\begin{gathered} \mu\pm z\cdot\frac{S}{\sqrt[]{n}} \\ 73.1\pm2.576\cdot\frac{16.5}{\sqrt[]{29}} \\ 73.1\pm7.893 \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/y44ycnelaqpfptwvibxiscxhwlgnh3k7qy.png)
If we write this as a tri-linear inequality we have: