The car, starting from rest on a ramp, accelerates with a constant rate. After 1.80 seconds, its final position is 2.28 meters from the initial position, given an average velocity of 1.20 m/s.
To find the final position of the car, you can use the kinematic equation that relates initial position
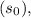 final position
final position
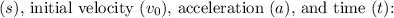
![\[ s = s_0 + v_0 t + (1)/(2) a t^2 \]](https://img.qammunity.org/qa-images/2022/formulas/physics/college/w1dtj5fivo9jjeajh0bwia.png)
Given:
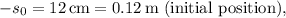
-
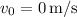 (initial velocity, as the car starts from rest),
(initial velocity, as the car starts from rest),
-
 is the acceleration,
is the acceleration,
-
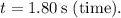
Since the car starts from rest, the initial velocity
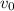 is 0.
is 0.
The average velocity
 can be calculated using the formula:
can be calculated using the formula:
![\[ v_{\text{avg}} = \frac{\text{change in position}}{\text{change in time}} \]](https://img.qammunity.org/qa-images/2022/formulas/physics/college/j21ljco5an901wr7zi3fei.png)
![\[ v_{\text{avg}} = (s - s_0)/(t) \]](https://img.qammunity.org/qa-images/2022/formulas/physics/college/atytp5so11q6shqp8dyxtt.png)
You know
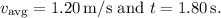 Solve for \(s\):
Solve for \(s\):
![\[ s = s_0 + v_{\text{avg}} t \]\[ s = 0.12 \, \text{m} + (1.20 \, \text{m/s})(1.80 \, \text{s}) \]\[ s = 0.12 \, \text{m} + 2.16 \, \text{m} \]\[ s = 2.28 \, \text{m} \]](https://img.qammunity.org/qa-images/2022/formulas/physics/college/xr3kri2c1frnlbujt9ta58.png)
So, the correct final position of the car is
 .
.