Question

Find the vertex and then determine if the graph opens up or down. Find any intercepts and sketch a graph

Answer 1

In order to find the vertex, first let's identify the coefficients a and b from the standard form:

`\begin{gathered} y=ax^2+bx+c\\ \\ y=-x^2+6x-11\\ \\ a=-1,b=6,c=-11 \end{gathered}`

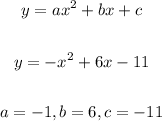
Now, let's calculate the x-coordinate of the vertex with the formula below:

`x_v=(-b)/(2a)=(-6)/(-2)=3`

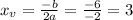
To calculate the y-coordinate of the vertex, let's use the x-coordinate of the vertex in the equation:

`\begin{gathered} y_v=f(x_v)=-3^2+6\cdot3-11\\ \\ y_v=-9+18-11\\ \\ y_v=-2 \end{gathered}`

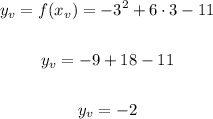
Therefore the vertex is located at (3, -2).

Since the coefficient a is negative, the graph opens downward.

The y-intercept is (0, c), that is, (0, -11).

The x-intercepts are the zeros of the function:

`\begin{gathered} x=(-b\pm√(b^2-4ac))/(2a)\\ \\ x=(-6\pm√(36-44))/(-2)\\ \\ x=(-6\pm√(-8))/(-2) \end{gathered}`

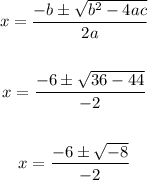
Since the zeros are complex numbers, there are no x-intercepts.

To graph the equation, we can determine some ordered pairs that are solutions to the function and then graph a parabola passing through the points.

Using the points (0, -11) and (3, -2), we have: