Question

Use the empirical rule to solve the problem.At one college, GPA’s are normally distributed with a mean of 2.7 and a standard deviation of 0.4z what percentage of students at the college have a GPA between 2.3 and 3.1? Round to the nearest percentA. Almost allB. 68%C. 84%D. 95%

Answer 1

Empirical Rule in Statistics states that almost all (95%) of the observations in a normal distribution lie within 3 Standard Deviations from the Mean.

From the exercise we have

`\begin{gathered} \mu=2.7 \\ \sigma=0.4 \end{gathered}`

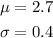
With these values we can find the intervals at 1, 2 and 3 sigma

1 sigma = 68%

`\begin{gathered} 2.7+0.4=3.1 \\ 2.7-04=2.3 \\ \end{gathered}`

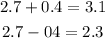
For 68% the interval is between 2.3 and 3.1

2 sigma=95%

`\begin{gathered} 2.7+2(0.4)=3.5 \\ 2.7-2(0.4)=1.9 \end{gathered}`

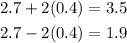
For 95% the interval is between 1.9 to 3.5, this interval is already very wide

We can see that at 1 sigma is the exact range of students who have 2.3 to 3.1 in their GPA. That is, the answer is 68%