This problem is about simply probabilities, that is, the ratio between the number of events and the total number of outcomes. In this problem, we have to find P(B), which indicates the probability of event B. Additionally, we know by given that event B is defined as "choosing an odd number", where the total number outcome is 10, because the whole set is from 1 to 10. So, the probability P(B) is:
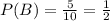
Therefore, the probability of event B is 1/2 or 50%.
On the other hand, part B indicates that we must find the probability of events A and B. Remember that the intersection sign indicates multiplication. So, we need to find the probability of A, to then multiply it with P(B):
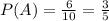
Therefore, the probability of choosing a number less than 7 is 3/5, because there are only 6 numbers less than 7.
Now, we find the intersection:

Therefore, the probability of event A and B happening is 30%.
The third probability we have to find is the probability of the complement set of B, that is, all numbers which are not included inside B, but in the Universe. Those numbers are 2, 4, 6, 8, and 10. So, the probability would be:
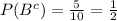
Therefore, the probability of the complement set of B is 1/2 or 50%.