Part A.
To find the expected value, first, we find the probability of the event: a student that uses a password.
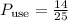
Then, we multiply this probability by the number of students 275 to find the expected number
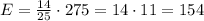
The number of students expected to use passwords is 154.
Part B.
It's important to know that a sample has to be good enough in order to represent the population. In this case, a sample of 25 students out of 250 is not enough representation. Also, there's no random sampling process implemented.
Hence, the answer is: No; The sample size is small and not randomly selected.