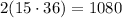Question

Write an equation that represents the following situation. Then, solve the equation. 1) A quilt design is made up of right triangles that have a base of 6 in and a height of 2 in. If the quilt is rectangular with dimensions of 90 in by 72 in, how many triangles are needed to complete the quilt? (Hint: Draw pictures of the shapes and label the dimensions.) a. Write the equation in words. b. Calculate the two areas. = 4 = c. Choose a variable for the unknown quantity and write the equation with the substituted values. d. Solve the equation. Include appropriate units in your answer.

Answer 1

We will solve as follows:

*First: We determine the minimum number of triangles that should go in a row [Taking into account that there will be 1 empty triangular space of identical measurements but rotated 180°], that is:

*We determine the minimum number of triangles of the base dividing the length of the base of the rectangle by the length of the base of the triangle:

`(90)/(6)=15`

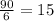
So, from this we will have that we would need 15 triangles for the base.

*We determine the number of triangles for the heigth of the rectangle:

`(72)/(2)=36`

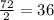
*Now, we determine the total number of triangles we would need:

`30\cdot36=1080`

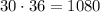
So we would need 1080 triangles to create the whole rectangular shape.

a) The equation:

`2t=(90)(72)`

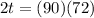
Here "t" represents the number of triangles needed on the horizontal line and in the vertical line, but not taking into account the empty spaces due to them being triangles.

b)The area of the triangle:

`A_1=6\cdot2\Rightarrow A_1=12`

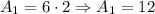
The area of the rectangle:

`A_2=90\cdot72\Rightarrow A_2=6480`

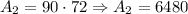
c)The variable for the unkown quantity is "t".

d)We solve the equation.

`2(15\cdot36)=1080`