Question

The distance that an object falls from rest, when air resistance is negligible, varies directly as the square of the time that it falls (before it hits the ground). A stone dropped from rest travels 304 feet in the first 6 seconds. How far will it have fallen at the end of 7 seconds? Round your answer to the nearest integer if necessary.

Answer 1

Since the distance varies directly as the square of time, then its expression looks like this:

`d\text{ = k}\cdot t^2`

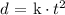
Where d is the distance, "k" is the proportionality constant and t is the time the object is falling. We know that after 6 seconds the stone travels 304 feet. With this information we can determine the value of "k".

`\begin{gathered} 304=k\cdot(6)^2 \\ 304=k\cdot36 \\ k=(304)/(36) \\ k=8.44 \end{gathered}`

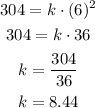
Therefore the complete expression is:

`d=8.44\cdot t^2`

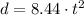
We want to know the distance after 7 seconds, therefore t = 7.

`\begin{gathered} d=8.44\cdot(7)^2 \\ d=8.44\cdot49=413.56\text{ feet} \end{gathered}`

The stone will travell approximatelly 314 feet in 7 seconds.