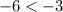Question:
Solution:
Remember that the equation of a line is given by:

where m is the slope of the line. Now, the given line is:
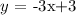
thus, the slope of this line is m= -3. Now, the problem asks us to find which of the given relationships represents a function with a lesser slope than the given line. To do this, remember that the slope of a line is given by the following equation:
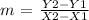
where (X1, Y1) and (X2,Y2) are points on the line or data in a file of the table that represent a line.
therefore, we are going to calculate the slope for each relationship given in the problem:
For A:
(X1,Y1) = (0,-1)
(X2,Y2)= (-1,5)
then the slope is:
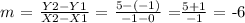
note that
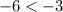
For B:
(X1,Y1) = (-6,-3)
(X2,Y2)= (-4,-1)
then the slope is:
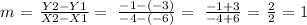
note that:
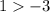
For C:
(X1,Y1) = (-1,2)
(X2,Y2)= (-2,3)
then the slope is:

note that:
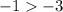
Finally:
For D:
(X1,Y1) = (-4,7)
(X2,Y2)= (-2,1)
then the slope is:
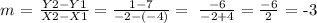
note that:
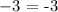
so that, we can conclude that the correct answer is A:
that is because the slope of graph A is lesser than the given line: